[LG Aimers] 지도학습(분류/회귀) 2 - Linear Regression/Gradient Discent
LG Aimers 학습 내용을 정리한 글입니다.
1. Linear Regression : 주어진 입력에 대해 출력과의 선형적인 관계를 추론
선형 model이라고 해서 반드시 입력 변수가 선형일 필요는 없다.
Minimizing MSE
최적화 파라미터: cost function을 가장 최소화
Gradient descent: 여러번 iterative하게 최적 parameter를 찾아가는 과정, n is large
Normal Equation: 1 step으로 해를 구함
2. Gradient Discent
Gradient : the derivate of vector functions( partial derivative along each dimension)
→ 함수의 변화량이 가장 큰 방향으로 update를 진행한다.
step size α : parameter update에 변화 정도를 조정하는 값
→ 학습 이전에 설정하는 hyper parameter
→ loss가 변화하는 정도를 보인다.
θ : learnable parameter
→ 구하고자 하는 모델의 학습 파라미터
Batch gradient descent의 단점 : 한번 update를 할 때마다 전체 샘플 m의 error를 고려한다.
→ 데이터 샘플이 많아질수록 복잡도가 굉장히 커진다.
Stochastic gradient descent(SGD) : 샘플 m을 극단적으로 줄여 1로 설정
→ iteration을 빠르게 돌지만, 노이즈의 영향을 받기 쉽게 된다.
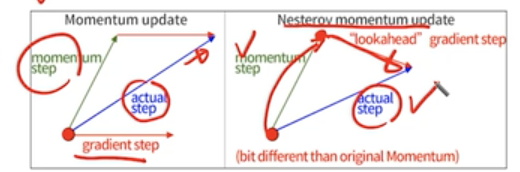
SGD + momentum : Use a velocity as a weighted moving average of previous gadients
nestrov momentum : lookahead gradient step이용 (gradient를 먼저 평가하고, 업데이트를 한다.)
AdaGrad : 각 방향으로의 learning rate를 적응적으로 조절하여 학습 효율 ↑
→ gradietn값이 누적됨에 따라 learning rate 값이 굉장히 작아지게 된다. (학습이 그 지점에서 일어나지 않는다.)
RMSProp : AdaGrad의 단점을 보완한 방식으로 어느정도 완충된 형태로 학습 속도가 줄어든다.
Adam(Adaptive moment estimation) : RMSProp + Momentum
: 1. Compue the first moment from momentum
2. Comput the second moment from RMSProp
3. Correct the bias
4. Update the parameters
Learning rate scheduling :
Learning rate: key hyper parameter for gradient-based algorithms ( need to gradually decrease learning rate over time)
Model 과적합 문제 : Model이 지나치게 복잡하여, 학습 Parameter의 숫자가 많아서 제한된 학습 샘플에 너무 과하게 학습이 되는 것
해결→ Regularization 방식